データサイエンス(統計学)を勉強して学んだことをまとめていきます。最初は、統計とは、から始まり、平均や中央値など基本的な統計量の説明をしていきます。
統計とは
「集団における個々の要素の分布を調べ、その集団の傾向、性質などを数量的に統一的に明らかにすること。また、その結果として得られた数値。」 広辞苑より
データ
データの種類
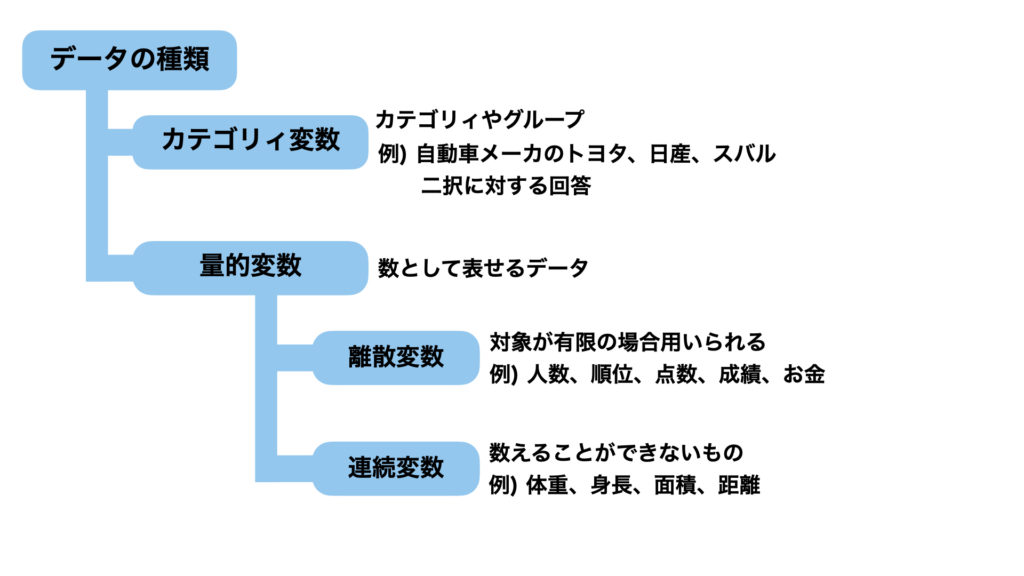
データには大きく分けて二つに分けられます。その二つはデータの種類と測定尺度です。さらに、データの種類にはカテゴリィ変数と量的変数に分けられます。
カテゴリィ変数はカテゴリィやグループを表し、自動車メーカのトヨタ、日産、スバルなどがカテゴリィ変数になります。また、二択に対する回答もカテゴリィ変数になります。例えば、車を持っているかという質問に対し、「はい」や「いいえ」といった回答を得ることができます。こういったものもカテゴリィ変数となります。
量的変数は、数として表せるデータのことを指します。さらに、量的変数は離散変数と連続変数に分けることができます。離散変数は対象が有限の場合に用いられます。例えば、赤ちゃんの数や順位や点数、成績などがあります。連続変数は数えることができないものを指します。例えば、体重や身長、面積、距離などがあります。
測定尺度
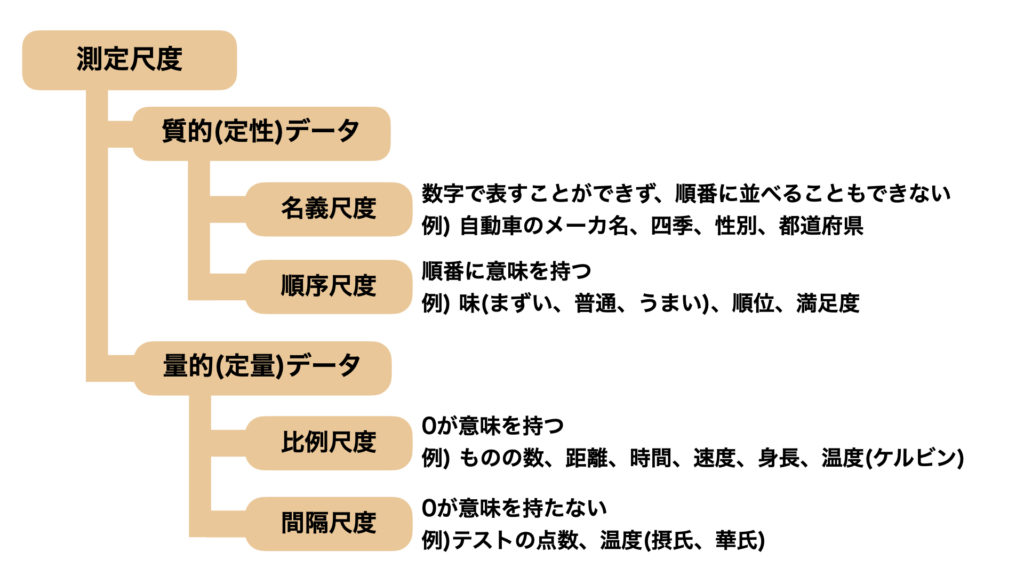
測定尺度は、質的(定性)データと量的(定量)データに分けられます。また、質的データは名義尺度と順序尺度に分けることができ、量的データは間隔尺度と比例尺度に分けることができます。
名義尺度とは、上記でも出てきたような、トヨタや日産などの車のメーカー名や四季などがあります。これらは、数字で表すことができず、順番に並べることもできません。他にも、性別や人種、都道府県などがあります。
順序尺度とは、順番に意味を持つデータのことをいいます。例えば、ランチを食べて味を評価する場合、ひどい、普通、美味しいと評価をする時、この評価を定量的に表すことはできませんが、ひどいというマイナスから美味しいというプラスまで順番があることがわかります。こういったときのデータを順序尺度と言います。
比例尺度とは0が意味を持つ、少し言い換えると、0が「何もない」、つまり基点(原点)として特別な意味を持つデータをいいます。データが比例の関係にあることを意味しています。例えば、ものの数や距離、時間が比例尺度にあたります。
間隔尺度は0が意味を持たない、言い換えると、0という値が「何もない」状態を意味していない(値のひとつにすぎない)データをいいます。例えば、気温(摂氏と華氏)やテストの点数などがあります。
比例尺度と間隔尺度を理解するための小話で、温度を表す単位には摂氏(℃)、華氏(℉)、ケルビン(K)があります。摂氏0℃も華氏0℉も、0には意味を持たず、これは人があくまでも利便性のために作ったものです。しかし、ケルビンの場合、0Kというのは、分子の運動が完全に止まる時で、これ以上小さい値をとることはありません。つまり、ケルビンは0が意味を持つので、比例尺度となります。一方、摂氏と華氏は0が意味を持たないので、間隔尺度になります。
母集団と標本
母集団と標本(サンプル)
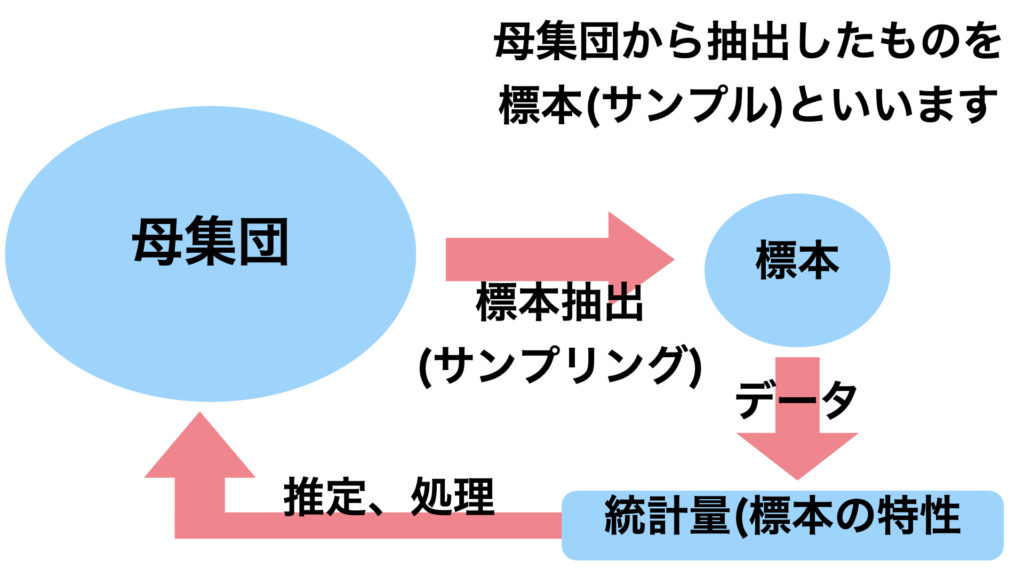
母集団とは調査対象の全てのデータのことをいいます。母集団から抽出したものを標本(サンプル)といいます。母集団はその範囲を規定するのが難しく、データを全て集めるのは困難です。そこで、範囲を規定しやすく、データを集めやすい標本がよく使われます。データ分析では母集団から標本を抽出し、標本を使い、そこから母集団の特徴を推定します。
標本を集めるためにはそのデータが正確でなければいけません。この場合の、正確というの言葉の意味は、その標本がランダム性と代表性を満たしているということです。
ランダム性とは、標本の要素が完全にランダムに選ばれているかどうかという意味です。
代表性とは、母集団から選ばれた標本が、調査対象者全体の結果を偏りなく正確に反映できているかどうかを意味します。
ランダム性と代表性とは何かを例を上げて見てみましょう。
例えば、T大学の生徒の学習時間を調べるために、T大学の食堂にいる学生にインタビューをしました。この時の標本の抽出の仕方はランダム性と代表性を満たしているでしょうか。答えはどちらも満たしていません。
ランダム性に関して言えば、大学の食堂でインタビューをしているので、食堂にこない学生は標本に含まれない可能性が高いです。なので、これはランダム性を満たしていません。
次に、代表性ですが、大学の食堂ではT大学の学生以外も使用できるため、その対象は母集団である、T大学の学生とは限らないからです。なので、代表性も満たしていません。
では、どのようにしたら、正確な標本を集められるでしょうか。一番いいのは、データベースにアクセスし、そこからランダムに学生を選ぶことです。このようにすれば、ランダム性と代表性を満たす標本を集めることができます。
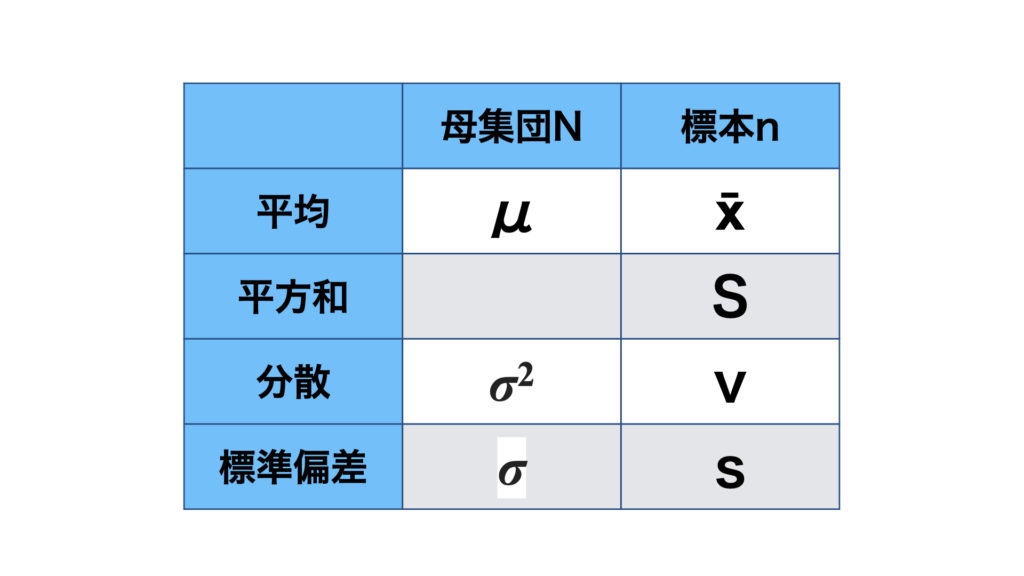
母数と統計量
母数とは、母集団の分布を特徴付ける値です。母集団と標本ではそれぞれの平均などを表す記号が違うので、気をつけましょう。それぞれの詳しい求め方などは次の記事に書きます。